Multivariable Calculus and Classical Physics problems
Posted on 09 Mar 04:47 | by BaDshaH | 1 views
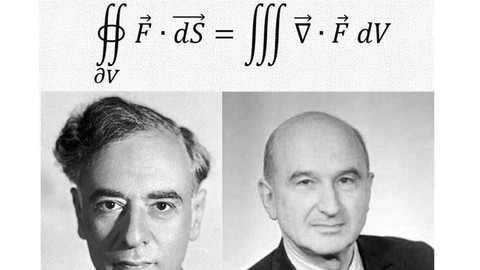
Last updated 10/2023
Duration: 15h 32m | Video: .MP4, 1920x1080 30 fps | Audio: AAC, 48 kHz, 2ch | Size: 16.1 GB
Genre: eLearning | Language: English
Intuition for Multivariable Calculus and how to use it to solve classical physics problems
What you'll learn
how to intuitively understand Multivariable Calculus by using the mathematics
Divergence theorem (how to prove it)
Stokes theorem (how to prove it)
Multiple integrals
line integrals
Surface integrals
Jacobian
How to tackle graduate-level problems in classical mechanics
the kinematics of rigid bodies
How to deal with non-inertial frames of reference
How to calculate the angular velocity of a rigid body
How to calculate the frequency of small oscillations
How to analyze the dynamics of rigid bodies
How to calculate the inertia matrix and moments of inertia
How to construct a Lagrangian in classical mechanics
The importance of the Lagrange formalism
How to derive the Hamiltonian (energy) of a system
Requirements
Single Variable Calculus
Description
In the
first
part of this course Multivariable Calculus is explained by focusing on understanding the key concepts rather than learning the formulas and/or exercises by rote. The process of reasoning by using mathematics is the primary objective of the course, and not simply being able to do computations. Besides, interesting proofs will be given, such as the Gauss and Stokes theorems proofs.
The prior knowledge requirement is Single variable Calculus (even without a great mastery of it).
I will list some of the most important concepts that we will see here in the following.
partial differentiation
. The partial derivative generalizes the notion of the derivative to higher dimensions. A partial derivative of a multivariable function is a derivative with respect to one variable with all other variables held constant. Partial derivatives may be combined in interesting ways to create more complicated expressions of the derivative. For example, in vector calculus (which we will see), the "del" operator is used to define the concepts of gradient, divergence, and curl in terms of partial derivatives. A matrix of partial derivatives, the Jacobian matrix, may be used to represent the derivative of a function between two spaces of arbitrary dimension. Differential equations containing partial derivatives are called partial differential equations or PDEs. These equations are generally more difficult to solve than ordinary differential equations, which contain derivatives with respect to only one variable (PDEs are not discussed in this course).
Multiple integration.
The multiple integral extends the concept of the integral to functions of any number of variables. Double and triple integrals may be used to calculate areas and volumes of regions in the plane and in space.
The surface integral and the line integral are used to integrate over curved manifolds such as surfaces and curves. We will see these concepts.
I am available for questions, which I could answer by (possibly) uploading new content to the course, namely videos containing the solution.
The
second
part of this course is about solving advanced mechanics problems;
since multivariable calculus is a staple of this second part, I decided to combine the part on physics problems and the one on multivariable calculus into a single course
, where you can therefore find lots of material. This set of problems is taken from the first volume of the course of theoretical physics by Landau and Lifshitz. I have selected some problems from this book and provided a thorough step-by-step solution in the course; the solutions to these problems are also given in the book but they are usually quite terse, namely not many details are provided. Therefore, what we will do in the course is to first construct the necessary theory to deal with the problems, and then we will solve the problems. Some theory is also discussed while solving the problems themselves. Every single formula in this course is motivated/derived.
We will start from the action principle, whose main constituent is the Lagrangian, which is fundamental to dealing with advanced problems in all branches of physics, even if we restrict ourselves to mechanics in this case. We will solve several problems related to how to construct a Lagrangian of a (possibly complex) system, and we will also derive the Hamiltonian from the Lagrangian, which represents the energy of a system, and do some problems on that.
We will also study the kinematics of rigid bodies, and derive formulae for the velocities of points which belong to the bodies, as well as formulae for accelerations. Accelerations are important not just for kinematics, but also for the dynamics of rigid bodies.
As regards the motion of rigid bodies, we will discuss the kinetic energy, which is necessary to obtain the Lagrangian, and solve several problems in three dimensions related to how to find the kinetic energy of a body in motion.
The expression of the kinetic energy is dependent on the angular velocity (which is a concept that we will derive in kinematics), and also depends on the inertia matrix (or inertia tensor), which we will also derive. The formulae will be therefore written in a very general form, and this is useful when tackling difficult problems, since knowing a general method will provide the means to solve them.
The inertia tensor will appear in the expression for the kinetic energy, and it will also appear in dynamics, in the formula for moments; we will see why it appears, and use the theory to solve problems.
We will also discuss non-inertial frames, and find the deflection of a freely falling body from the vertical caused by the Earth's rotation (which makes the Earth a non-inertial frame).
Who this course is for
Students who are interested in mathematical reasoning and derive the most important concepts of Multivariable Calculus
Students who would like to learn the most general formalism to tackle advanced problems in classical mechanics
Homepage
https://www.udemy.com/course/mathematical-intuition-behind-multivariable-calculus
https://rapidgator.net/file/9398e7970f1286b46fb78261cb805438
https://rapidgator.net/file/d5943ec39ed6d6b033fadac086880674
https://rapidgator.net/file/13764c236e3c1fb4175a50575c39f9bf
https://rapidgator.net/file/2d6a702b57dbd96d767dd674d14c8d0a
https://rapidgator.net/file/a15328364b857086f189885620832de1
https://rapidgator.net/file/8d7085770b3a4c258eff46fbb0578cdd
https://rapidgator.net/file/4e6e7c14b40cb1982f8cb9f2203e525c
https://rapidgator.net/file/77b437eb427057a861b70bfc4f7c49a9
https://rapidgator.net/file/b27406029a4287896221a0a0892b1501
https://rapidgator.net/file/37efcd37d39ee1d03906c61e11d20ad3
https://rapidgator.net/file/597801cfb638b4c357065ced0f65e480
https://rapidgator.net/file/414b7113977996757e1a25051d9320fa
https://rapidgator.net/file/72ddd24a3845ed62c52a17ac246a0275
https://rapidgator.net/file/4364b024c6ca4d83ec4e1ca845103642
https://rapidgator.net/file/a669e990c0e4491bf5d87dd32ca7b993
https://rapidgator.net/file/29b3bc5cec188e1e07ff7c3b02b3bc63
https://rapidgator.net/file/427e2ad627cb3137fb4c37d542b4ac66
https://nitroflare.com/view/17E76A08C0FC415
https://nitroflare.com/view/43B89A7D7364382
https://nitroflare.com/view/1E68034345BA7E9
https://nitroflare.com/view/0986977C04F8C2B
https://nitroflare.com/view/3B923384DD37A6E
https://nitroflare.com/view/F240EA90D63290F
https://nitroflare.com/view/003B996A3BB77E3
https://nitroflare.com/view/62ACD41BC96565E
https://nitroflare.com/view/2E80822EB9E8DB2
https://nitroflare.com/view/9E36F935C0CEC9A
https://nitroflare.com/view/61A04EA981B867E
https://nitroflare.com/view/61CE581F09912EB
https://nitroflare.com/view/F584DB488762A75
https://nitroflare.com/view/8F830B50BD3BB78
https://nitroflare.com/view/735F031C7FC507A
https://nitroflare.com/view/C03F77E409B2208
https://nitroflare.com/view/44C33F5922C1C6C
https://ddownload.com/0hx25on3q0mh
https://ddownload.com/uy825izb8xai
https://ddownload.com/cort93d81915
https://ddownload.com/s2nfjpu479n0
https://ddownload.com/ntzlxyv2d6yb
https://ddownload.com/3naklv36eng2
https://ddownload.com/sm35sgj2j5td
https://ddownload.com/qvfiq5hl9yot
https://ddownload.com/3womx148zalt
https://ddownload.com/ctclqvqesfdv
https://ddownload.com/g79kuvdblw6v
https://ddownload.com/yj6ymbf87fmf
https://ddownload.com/6xf07svtg3on
https://ddownload.com/e9vo6u46np2i
https://ddownload.com/ksee1mx32avt
https://ddownload.com/fej9z8sjt9kv
https://ddownload.com/2fkzlesropib
Related News
System Comment
Information
 Users of Visitor are not allowed to comment this publication.
Users of Visitor are not allowed to comment this publication.
Facebook Comment
Member Area
Top News